Visualización de la definición de π. Es el perímetro de una circunferencia de diámetro 1.

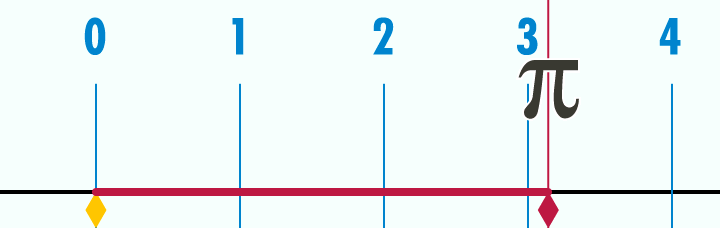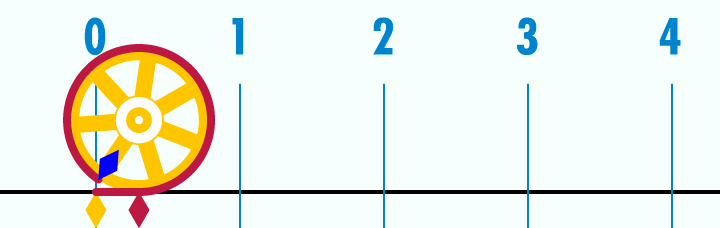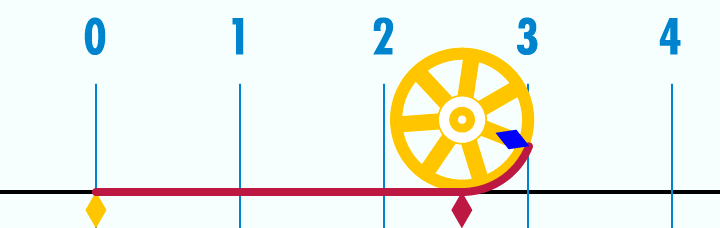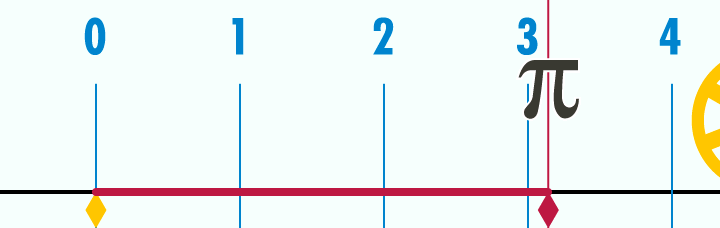
Método de Arquímedes para encontrar dos cotas que se aproximen al número π.

Arquímedes (siglo III adC), fue capaz de determinar el número π entre el intervalo comprendido por 3 10/71 como valor mínimo y 3 1/7 como valor máximo. Con esta aproximación de Arquímedes se llegaba a un valor con un error entre 0.024% y 0.040% sobre el valor real. El método empleado por Arquímedes[8] era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.

Arquímedes (287-212 BC) averiguó que 3 10/71 > 3 * 1 / 7

http://www.uam.es/personal_pdi/ciencias/ezuazua/informweb/trabajosdehistoria/ARQUIMEDEScirculoesferacilindro.doc

La razón de la circunferencia de un círculo cualquiera a su diámetro es
3 ( 10/71 ) > 3.142857... )

Arquímedes busca la razón de la circunferencia. Para hallarla utiliza como siempre los polígonos regulares inscritos y circunscritos, con una excepción, en vez de considerar sus áreas, se centra en sus perímetros.

Empieza con el hexágono regular inscrito en un círculo. Arquímedes sabía que cada lado del hexágono era igual al radio del círculo, es decir,

p = (^{Circunferencia del círculo}/ _{Diámetro del círculo}) > (^{Perímetro del hexágono} / _{Diámetro del círculo}) = ^6r/_2r = 3

A continuación, duplicó el número de lados del polígono inscrito para obtener un dodecágono, aquí surgió el primer problema, ya que para calcular el perímetro necesitaba obtener Ö3. Así es como Arquímedes sorprende de nuevo a los matemáticos modernos, dando la siguiente aproximación ^*:

²⁶⁵/₁₅₃ < Ö₃ < ^1.351/₇₈₀

*Se desconoce como llegó a esta aproximación.

Arquímedes continuó dividiendo por la mitad los lados del dodecágono, para obtener un polígono regular de 24 lados, luego de 48 y finalmente de 96. En cada cálculo tuvo que aproximar raíces cuadradas. Al llegar al de 96 lados obtuvo:

p = (^{Circunferencia del círculo}/ _{Diámetro del círculo}) >

(^{Perímetro del polígono de 96 lados} / _{Diámetro del círculo)} > ⁶³³⁶/_{2017 (1/4)} > 3 (¹⁰/₇₁)

Arquímedes cambió el razonamiento y realizo cálculos similares para los polígonos circunscritos 12, 24, 48, 96 lados. De esta manera halló el límite superior de p = 3 ( ¹/₇ ).